Dos sudokus diferentes con igual celdas-pista

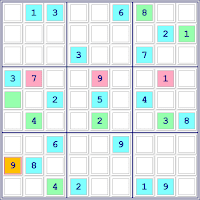
Los dos ejemplos de sudoku para esta demostración (no científica, es apenas un caso), los hice pensando en que ambos juegos tuvieran el mismo número de pistas y que, además, las celdas que contuvieran las pistas estuvieran ocupando exactamente los mismos lugares de la rejilla.

Me costó bastante elaborar un segundo tablero con estas condiciones pero finalmente lo logré. 

Las pistas son 27 en cada sudoku. Ambos son simétricos y tienen una solución única. ¿Qué más? Ah, sí: no sustituí un número de un sudoku por otro, tampoco son equivalentes. Los resultados de uno con respecto al otro son esencialmente distintos. Con la excepción de que comparten 13 celdas con los mismos datos: seis de ellos se encuentran en las pistas, los otros siete se hacen evidentes al solucionarlos.

Otro aspecto importante es que tienen diferente nivel de dificultad. Eso no lo trabajé, ni creo que en este momento yo pudiera lograrlo a voluntad...

Tablero de Sudoku con celdas-pista y comunes coloreadas

En esta ocasión el tablero vacío con las celdas coloreadas es para comparar la información clave en ambos sudokus: De las 27 celdas-pista, 21 están en azul y 6 en amarillo. Estas seis celdas amarillas y las otras siete coloreadas en rojo tienen los mismos números. 

Sudoku No.1 (27) pistas 

Sudoku No.6 (27 pistas)

Para demostrar que los números no se sustituían unos con otros, al crear el segundo tablero coloqué dígitos diferentes en las celdas que correspondían a un mismo número del primer sudoku. Como ejemplo veamos el 9 que aparece cuatro veces en el Sudoku No.1 y lo substituí por 5, 2, 7 y 6 en el Sudoku No.6.

Solucionar el sudoku No.1 es más sencillo que el No.6 pero con la información de las celdas en rojo se puede resolver también muy fácilmente. 

En este ejercicio me interesaba ver si a partir de 27 celdas-pista coincidentes en ubicación podían obtenerse dos sudokus distintos, tanto en el orden y la dificultad al resolverlo como en el llenado completo de la rejilla con números diferentes. (En este caso sólo logré 68 números diferentes... los otros 13 ocupan las mismas celdas; 6 de ellos eran parte de los números pista...).

Tres sudokus, un tablero

¿Cómo saber si un sudoku es igual a otro, o diferente?
No me refiero a los que se generan cuando se rota el tablero, se intercambian bandas o se sustituye un número por otro en las casillas para determinar su similitud. 

La pregunta va más allá. ¿Qué lo define? ¿Cuál es la clave para determinar la identidad de un sudoku? Podrían ser las pistas, pues son elemento fundamental para resolverlo; el grado de dificultad; las celdas ocupadas; la solución;  las estrategias para solucionarlo.

Por el momento esta inquietud la cristalicé con un ejercicio curioso. Aquí muestro tres tableros sudoku simétricos, con solución única cada uno y diferencias claramente visibles en los aspectos mencionados anteriormente.
Cada uno de estos sudokus, así como se muestran, tiene una solución.
Tuve especial cuidado al generarlos, para evitar que compartieran celdas-pista lo más posible. Hay cinco (amarillas en el tablero en rojo) comunes a dos tableros, pero el resto de las casillas llenas no se empalma en los tres sudokus.

Si los observamos con cuidado apreciamos que la cantidad de pistas es diferente en cada uno; las celdas ocupadas tampoco son las mismas, y los tres tienen diferentes números-pista en las celdas con las mismas coordenadas (cf). 

Para "verlos" con más claridad y destacar su ubicación en el tablero, coloreé de amarillo las 25 celdas-pista del primer Sudoku; en azul las 28 celdas pista del segundo; y en las del tercer sudoku (27 pistas) 22 celdas son rojas y 5 amarillas, además tiene 6 celdas sin número, en verde. 

Si vaciáramos los números pista de cada sudoku en el tablero vacío, veremos que se pueden acomodar perfectamente todas las pistas amarillas, todas las pistas azules y también las rojas. ¡Sin estorbarse! En el tablero sólo quedarían 6 casillas vacías, las verdes, que pudieron marcarse de rojo (o azul, o amarillo) pero no eran pistas clave.

La pregunta es: ¿Cuántos sudokus distintos son? 

Los números que en este ejercicio completarían el tablero vacío, ¿Son la solución única para cada uno de estos tres sudokus? ¿Cumplen con las reglas de no repetir el dígito en columna, fila y subcuadrícula?

Y, si así fuera, ¿Demuestra eso que son un solo sudoku? ¿o son tres? 

                   

Sudoku simétrico 25 pistas 

Sudoku simétrico 28 pistas

 

Sudoku simétrico 27 pistas

                      

                           tablero de sudoku  "vacío"  

Sudokus a mano

Este fin de semana lo pasé intentando crear sudokus simétricos, a mano, y con la menor cantidad de números dados. 

En los tres que trabajé, obtuve 25 pistas. Por más que me esforcé, no pude disminuir esa cantidad. El último sudoku me llevó más tiempo que los otros. Pues no encontraba soluciones y debí regresar varias veces a reiniciarlo. Cuando finalmente llené el tablero, y empecé a despejarlo para dejar sólo las pistas necesarias, también tuve que buscar opciones una y otra vez. Primero requería 29 pistas, logré bajarlas a 27 y, finalmente, tras muchos intentos, a 25. Fue más suerte que perseverancia, creo.

En esta parte del diseño empecé a trabajar con par de números en simetría... Pero igual que en la etapa de llenado, los primeros 18 dígitos que acomodé, ya no los muevo. No imagino de qué otra forma iniciar.

Estos 18 números que tomo como base deben incluir todos los dígitos del 1 al 9 al menos una vez. Y los nueve restantes los escojo a mi inspiración. Aunque trato de equilibrarlos en la segunda parte del llenado, si es posible.  Aquí todavía no considero la simetría. Es más importante ver cómo se van afectando las posibilidades de los candidatos para cada región. Primero marco todos los números que salen solos y después busco las celdas que van quedando con pocas opciones en subcuadrícula, columna o fila y trabajo con ellas. Antes de marcar otro número, veo si tienen coincidencias con otras celdas con pocos candidatos y le sigo por allí, cuidando de no eliminar totalmente un número que aún no tiene su lugar.

Quisiera decir que es más divertido, o interesante, diseñar el sudoku que simplemente resolverlo, pero no puedo. Los 4 sudokus que he hecho hasta el momento, son muy sencillos de completar. Todavía no he intentado aplicar las estrategias de solución, como xy-wing, a la inversa; espero que ésa sea una forma de complicarlos.

Estas son dos propuestas de pistas "simétricas" para el mismo tablero de Sudoku. La única diferencia en ambos son los números en celdas coloreadas. El de pistas color rojo (sudoku 3a) es algo difícil de resolver comparado con el de pistas en color azul (Sudoku 3b), que sólo necesita localizar números sencillos, descubiertos y ocultos. Curioso ¿verdad? La primera versión tenía 27 pistas (incluyendo las de las cuatro celdas coloreadas) y la solución es todavía más ágil. Igual que la del tablero de 26 pistas simétricas que resulta de quitar el 7:c5f5.

Sudoku 3a

Sudoku 3b

Crear un Sudoku

¿Cómo se elabora un sudoku? Desde que conocí este pasatiempo he querido saberlo. Así que busqué instrucciones en internet pero, salvo algoritmos para diseñarlos por computadora, no encontré nada que lo explique.

Sé que debe tener una solución única; entre 17 y 34 pistas; acomodadas simétricamente pues Nikoli agregó esa condición, y que los números no deberán repetirse ni en columna, fila o subcuadrícula en una retícula de 9x9 casillas. Pero hasta allí. 

Buscando comprender mejor este juego, hace unos días decidí "hacer" un sudoku a "mano". No sé por qué creí que estaba preparada para lograrlo... ¡vaya sorpresa! Tratar de acomodar primero todos los números 1, y después los números 2, pronto me bloqueó lugares necesarios para los demás valores. 

Decidí cambiar la estrategia y poner el tablero "de cabeza", como hacen los creadores de Nikoli. 

Así me quedé un buen rato, intentando imaginar qué es lo que ellos ven, o buscan, en esas horas laboriosas y productivas; qué estrategias y secretos descubren y se comparten al final (o durante) la jornada. Pero la revelación esperada no se hizo presente: sigo sin comprender los encadenamientos "evidentes" que forman la trama del juego. Y mi fantasía de trabajar en Nikoli también se desvaneció, pues la única reflexión que se me ocurría mientras miraba y miraba la retícula de 9x9 era sobre si debía anotar los números "de cabeza" a medida que fuera armando el sudoku. De no hacerlo así (me parecía), el sudoku volvería a estar derecho.

La experiencia de hoy fue diferente. Tampoco una revelación. Empecé por acomodar cada número en no más de tres lugares. Esto debiera darme un máximo de 27 celdas ocupadas y, con suerte ¿por qué no?, asunto resuelto. Estaba feliz intentando distribuir números por todas las subcuadrículas, cuando advertí que en algunas casillas quedaban demasiados candidatos, pero no los que necesitaba. ¿Volver a intentarlo? pensé desanimada. Borré todo menos las primeras nueve pistas que había anotado y empecé a buscar casillas con muchos candidatos, en ese momento descubrí que debía ser lo opuesto, necesitaba ocupar las casillas con menos candidatos y al mismo tiempo aplicar las estrategias avanzadas de solución de sudoku... ¡Y funcionó! No sé cómo, pero completé el tablero. Ahora ¡a desandar el camino! quitar números hasta dejar las mínimas pistas necesarias para poder jugar a resolverlo...

Aquí una aclaración, cuando comencé a proponer los números en la retícula, marqué con azul los primeros diecisiete que acomodé; con verde los siguientes dieciocho y un tercer grupo de seis con otro color, con la intención de apoyarme en ellos como pistas. Tras varios intentos para seleccionarlos finalmente logré el objetivo. Un sudoku "no simétrico" con 24 pistas y un resultado único. Volví a probar, quitar, agregar, cambiar, (sobre el mismo tablero resuelto) y obtuve un sudoku "irregular" de 23 pistas. Sintiéndome a un paso de la realización completa, seguí borrando y probando ahora buscando la simetría y aquí está el resultado:

Sudoku simétrico, 27 pistas, dificultad no especificada

Un sudoku simétrico de 27 pistas, con única solución, de dificultad no especificada, probablemente ultrasencillo.

En el resultado final, como puede verse, conservé las 17 primeras pistas, en azul. Cuidé que todos los números estuviesen al menos una vez (5 y 7). Al anotar los números en verde, (probé con los 18, de uno por uno), encontré que sólo 8 de ellos eran necesarios y lograba la solución de sudoku "no simétrico" de 24 pistas. Para volver simétrico el sudoku tuve que borrar el número de la celda verde vacía f5c1 (ver figura arriba) y agregar cuatro de las pistas propuestas del tercer grupo: los tres números en rojo y el amarillo. Éste 9 (f8c1) y el 9 de f9c8, son necesarios para lograr la simetría, pero quitarlos no afecta a la solución única del sudoku.

Sudoku: los números deben quedar solos

"Los números deben estar -o deben quedar- solos..." Es el significado (o la traducción, según dicen), de "Suji wa dokushin ni kagiru" nombre completo del juego ahora conocido como Sudoku.

Dado que originalmente, durante dos o tres décadas antes de ser llevado a Japón, este pasatiempo numérico se conoció como Number Place -algo así como: "acomoda los números" o "cada número en su lugar"-, me parecía evidente que el término propuesto por los japoneses implicaba algo más profundo; no tan claro y sencillo como el término norteamericano. ¿Tal vez una conceptualización distinta? En todo caso, no lograba identificarlo. La frase: deben quedar -o deben estar- me parecía una orden o instrucción que no se correspondía con mi enfoque al resolverlos. 

Sí, sabemos que hay que ocupar las casillas del tablero con los números del 1 al 9 evitando que se repitan en cada fila, en cada columna y en cada subcuadrícula de 3x3. Y, si lo realizamos correctamente, cada uno de los dígitos del 1 al 9  aparecerá exactamente "nueve" veces en la rejilla del Sudoku.

Pero, ese "no repetirse", ese "quedar aislado" de sus pares (que se busca con cuidado, atención y perseverancia durante todo el proceso), no me cuadraba con el perentorio "deben quedar solos", que me urgía a rechazar y quitar números como si se tratara de una pelea, en lugar de buscar posicionarlos. 

La inquietud no desapareció aunque tampoco me impidió continuar resolviendo sudokus, tanto en papel como en computadora. De todas formas, de vez en cuando pensaba en cómo podría interpretar  más adecuadamente el sentido de la frase.

Antes hablé de enfoque; no sé si sea la expresión correcta. Al resolver el sudoku en papel hay dos preguntas claves para mí. Inicio con ¿dónde puede ir este número? Y lo visualizo como si fuese una pieza de rompecabezas y lo trajera en la mano ¿lo puedo acomodar aquí? ¿no? ¿entonces..., acá? Cuando ya no encuentro respuestas con la pregunta anterior, intento pistas con ésta otra: ¿cuál número puede ocupar esta celda? A veces hay un sólo número posible, frecuentemente hay varios. Entonces, anoto candidatos; poco a poco.

En la computadora, en cambio, cuando necesito el marcado de candidatos no puedo elegirlos; el programa (Simple Sudoku) los actualiza continuamente, y me muestra todos los candidatos posibles para cada una de las celdas por llenar; o ninguno. Es un marcado excelente sólo que, para aclarar las pistas me obliga a cambiar de enfoque y agregar otra pregunta... Sí, ya se imaginan, se trata de vaciar las casillas, de excluir, rechazar, los que sobran: ¿cuáles candidatos "debo" quitar de esta celda?, ¿cuál número "debe" quedar solo? 

No sé si los japoneses pensaron en esta técnica de exclusión cuando rebautizaron el juego, pero a mí me hace sentido. Ahora.

John Welch: Systematic Sudoku

Systematic Sudoku (Human engineered Sudoku solving) es un blog iniciado en septiembre de 2011 por John Welch y que tiene entradas continuas desde entonces hasta la fecha. Esto hace un total de 68 meses si contamos el actual. (Muy cerca de 300 entradas... )

El autor es norteamericano y su blog está en inglés.  

Aunque cuando inicié mis búsquedas de información de sudoku encontré algunas referencias a este blog, lo dejé pasar pues me limitaba a información en español. Además, sus sudokus explicados me confundían con sus marcas, pues con frecuencia alarmante aparecían los candidatos repetidos dentro de una misma celda.

Busqué y encontré otras opciones, sin entender todo lo que este blog ofrecía.

Hoy me acerqué con ánimo de revisarlo y me llevé una gran sorpresa.

Systematic Sudoku es un trabajo meticuloso, y bien ordenado. Además de claro, lógico, metódico y en cierta medida (una vez que te familiarizas con los términos y conceptos que el autor emplea), fácilmente comprensible.

El propósito de John Welch es ofrecer "una" secuencia detallada de la solución para cada sudoku seleccionado, de manera que quede evidente la forma humana de resolverlo. Él insiste, y con absoluta razón, que los algoritmos de computadora solucionan a base de prueba y error, contrario a como lo hacemos las personas; y que es importante, para quienes estén interesados en el proceso lógico, poder identificar cada paso del procedimiento para validarlo como correcto.   

Evidentemente no he tenido tiempo de ver mucho material del que ha publicado, pero intenté familiarizarme con las nociones básicas y el método con que hace sus marcas. Y me gustó. 

Quiero decir que, en cierta forma, él hace los mapas de los caminos que usé (usamos) para resolver el juego. Y no necesitamos tener conocimientos especializados de informática para entenderlos. 

Welch reconoce y menciona los trabajos de otros autores y organizaciones como Frank Longo y Peter Gordon de Mensa, y valora sus demostraciones. Incluso actualiza sus entradas anteriores cuando hay una aportación que pueda incorporar.

El idioma podría ser un impedimento al inicio (te puedes apoyar con un traductor de Google), pero parece que las abreviaturas (simbología) que usa Sysudoku y los esquemas desglosados y muy visuales facilitan entenderlo. O tal vez no, no lo sé todavía, hay que averiguarlo.  

Esta es la dirección en la red: https://sysudoku.com/

Cómo encontrar XY-Wing en Sudoku

Este sudoku tiene resueltas 56 celdas y las estrategias básicas ya no ayudan. Es momento para recurrir al método XY-Wing para "eliminar candidatos". 

Hay que encontrar las "3 casillas pista"; con dos candidatos cada una, y una combinación de tres números entre ellas. Debemos enfocarnos únicamente en las celdas con dos candidatos. 

Como no sabemos cuáles números son los que nos van a servir, se observa y compara continuamente una celda con otra hasta encontrar una segunda casilla con un "número en común". 

a) Si la segunda celda está en la misma fila o columna pero en diferente caja (tipo 1 xy-wing), buscaremos la tercera celda en una tercera caja y la casilla con "candidato a eliminar" en una cuarta caja.

b) Si la segunda celda está en la misma caja pero en diferente fila y columna (tipo 2 xy-wing) buscaremos la tercera celda en una segunda caja. Y las casillas con "candidatos a eliminar" se buscarán en ambas cajas. No es frecuente, pero podría haber hasta 5 casillas con "candidatos a eliminar".

Casillas E4 (5,8) y D6 (2,5) en la misma caja, pero en diferente fila y columna, tienen el 5 en común. Debemos buscar, en una caja diferente, una tercera casilla con los otros dos números: (2,8), pero sobre la misma fila o columna de E4 o D6.

Esta búsqueda de las "tres casillas pista" se hace al mismo tiempo. Si no encontráramos una casilla en fila o columna con los candidatos 2 y 8, descartaríamos esta combinación e intentaríamos en otra caja. En este caso la celda D7 (2,8) completa la figura. Las "tres casilla pista" son: E4 (5,8), D6 (2,5), D7 (2,8); los tres números "seguros" para estas celdas son 2, 5, 8.

Antes de buscar la celda (o celdas) con "candidatos a eliminar", debemos determinar cuáles de las "tres celdas pista" son las de los extremos. Una de ellas D6, en color verde, es la que une a las otras dos; no puede ser extremo pues al mismo tiempo comparte caja con E4 y fila con D7. Estas últimas dos, en azul, son las "casillas pista extremos". 

   

E4 (5,8) y D7 (2,8), "casillas pista extremos" en azul, tienen en común el candidato 8, que deberá ir forzosamente en una de ellas; por tanto, las celdas que, en ambas cajas queden bajo la influencia simultánea de E4 y D7, deberán eliminar este candidato común (8), si lo tuvieran. 

En esta figura localizamos las 5 casillas con influencia simultánea de E4 y D7 (en amarillo), y vemos que sólo hay dos celdas -D4 (3,5,8) y E8 (4,8)- que contienen el candidato 8 y deberán eliminarlo.

Como podemos ver, al eliminar el candidato 8 de las casillas influenciadas (D4, E8), se destraba todo el sudoku. Al anotar en E8 el número 4, hay dos celdas que quedan con un sólo candidato y también se forman varios pares descubiertos.

XY-Wing: Estrategia para Sudoku difícil

En un sudoku, no basta con "comprender" cómo funciona la estrategia XY-Wing para eliminar candidatos o "saber" cuándo puedes (o debes) buscarla: Hay que localizar el patrón para aplicarla.

Primero hay que estar seguros de que ya no se puede ni anotar otro número, ni eliminar algún candidato. Entonces hay que enfocarse únicamente en las casillas con dos candidatos para poder encontrar, o identificar, tres celdas "pista" (A, B, C) que nos indiquen otra celda (o hasta 5) a la que le podremos eliminar un candidato más. 

Hay dos patrones XY-Wing. 

El más sencillo es cuando las casillas pista (A, B, C) forman tres de las cuatro esquinas de un cuadrilátero. La cuarta esquina será la celda a la que se le eliminará el candidato imposible. Dos celdas pista (A, B) están en la misma fila, y dos (B, C) en la misma columna -o sea, una (B) es el eje para las otras dos-, pero ninguna celda pista comparte la misma caja de 3x3 con ninguna de las otras, ni con la cuarta (D) que comparte fila con C y columna con A: están en 4 cajas distintas; sólo se puede eliminar un candidato.

En el otro patrón, los candidatos a eliminar podrían ser hasta cinco, de cinco celdas distintas; y tanto las casillas pista, (A, B, C) como las celdas con candidatos a eliminar se encuentran dentro de 2 cajas de 3x3, contiguas, vertical u horizontalmente, o con la otra caja entre ellas. 

En este patrón, una casilla pista A estará sola en una caja y estará alineada, en fila o columna, con una de las otras dos casillas pista B (o C), que comparten caja pero que, entre ellas, no pueden estar ni en la misma columna, ni en la misma fila. De este modo las tres casillas pista formarán un ángulo. Uno de los extremos de este ángulo será la casilla pista sola (A) y el otro extremo será la casilla pista C (o B) con la que no comparte fila o columna. El número candidato que las celdas extremo (A y C) tienen en común será el candidato que se buscará para eliminarlo de las casillas que reciban influencia de ambas celdas pista extremo (o sea de A y C). Y que puede estar en hasta cinco celdas dentro de las dos cajas.

A partir de aquí el sudoku se resuelve casi solo. 

CARACTERÍSTICAS DE LAS CELDAS PISTA

Las celdas pista A, B, C deben estar relacionadas entre sí por tres números, y cada una de ellas sólo puede tener dos de ellos. Por ejemplo: 1, 2, 3, serían los números y las combinaciones para las tres casillas serían: A 1-2, B 2-3, y C 3-1 

Si el número que se repite en las celdas extremo es el que debemos eliminar y en el segundo patrón de XY-Wing, A y C son las celdas extremo y los candidatos de A son (1-2) y los de C son (3-1), el número a eliminar en las casillas comunes a ambas celdas pista es el (1). 

Sudoku y los Marlins de Miami

Pregunta: ¿Qué tienen en común Kyle Barraclough, Nick Wittgren, Dustin McGowan, Brian Schneider, David Phelps, Mike Dunn, y J. T. Realmuto, además de jugar en las Grandes Ligas de Béisbol para el equipo de Miami Marlins en 2016 y la mayoría ser lanzadores relevistas?

Respuesta: Su afición por el sudoku. Y que formaron un equipo que compite entre sí por resolverlos... ¡durante la temporada de juegos! Al menos por dos meses...

La historia es de septiembre de 2016. 

Tim Healey, reportero del Sun Sentinel, nos lo revela en su publicación "Para los relevistas de los Marlins, hay un juego antes del juego: Sudoku". 

En julio de ese año, los Marlins jugaban en St. Louis contra los Cardenales. El primer día, durante el descanso, Barraclough y Mc Gowan hallaron el sudoku del diario local y lo resolvieron.  Al segundo día se les unió Nick Wittgren y el último día del juego el entrenador Schneider se sumó al grupo demostrando tener más habilidad que los tres lanzadores.

A partir de allí este pasatiempo numérico se integró a las habituales actividades de los relevistas previas a los juegos en los que participaban; con la característica de que se convirtió en un reto que tomaron muy en serio. Recordemos que a los beisbolistas no les gusta perder...

El equipo -dice el reportero- saca copias del juego que aparece en el USA Today -que varía en dificultad- y se sientan juntos, generalmente en el tiempo que queda entre el estiramiento de los lanzadores y la práctica de bateo. David Phelps, Mike Dunn (ahora con Colorado Rockies) y el catcher Realmuto se integraron a esta competencia que, aseguran, es el reto más estimulante del día... cuando no son llamados a jugar béisbol, claro. 

Las declaraciones que los jugadores le hicieron a Healey, su preocupación por solucionar el sudoku primero que los demás, la presión al ver que otros anotan y ellos tienen el cerebro bloqueado, la alegría de ver cuando alguno gana y la sorpresa de que haya quién tenga más habilidad, son creíbles y fácilmente comprensibles aún para los que "no" somos adictos al sudoku, ni deportistas profesionales.

Sudoku Diet: Delgado y sano

¿El Sudoku ayuda a adelgazar? Y si es así, ¿cuántos sudokus hay que contestar para bajar los kilitos que nos sobran? 

No sé. Parece que el cerebro consume 90 calorías por hora mientras los resolvemos, sin necesidad de ejercicio extra: sentaditos en la silla y con lápiz en mano. Claro que si al mismo tiempo comemos una galleta con chips de chocolate -56 cal-, ¡pues ya valió! Y además, ya entrados en eso de comer galletas, de seguro te comes más de una... 

Un texto publicado en Daily Mail por David Wilkes en 2009, menciona la investigación de Tim Forrester junto con un comentario de la British Dietetic Association.  Ambos dejan claro que, para satisfacer la necesidad de energía, el cerebro consume calorías, no grasa. Entonces no hay escapatoria: hay que hacer ejercicio y cuidar la alimentación.  

Por otra parte, Jay H. Green, en su libro "The Sudoku Diet: Creating Your Optimal Health Through Logic" (que incluye menús, consejos y juegos), relaciona la alimentación, la salud y el sudoku. Sin desatender la importancia de una buena dieta, asegura que iniciar un sudoku (o resolver una parte) antes de cada comida permite una mejor digestión, hace perder peso, mejora la salud, la vitalidad, la memoria, la claridad de pensamiento, la capacidad sexual y la conciencia; pues funciona como una técnica de relajación divertida (meditación activa, la llama).

Afirma que la disciplina, atención, conciencia, paciencia, lentitud, intuición, y confianza en sí mismo que aplicamos al resolver este pasatiempo lógico, generan emociones que producen sensación de logro y felicidad y que esa "nueva" inercia es la clave que nos permite llegar relajados y disfrutar de los alimentos, con la consecuencia de una salud óptima. 

Aparentemente sólo necesitas un lápiz, un sudoku y "tu cerebro" antes de cada comida.

Trump, Jerry Martin y las capacidades para resolver un sudoku

Mi intención original, al iniciar el blog de sudoku, era comprender cómo funciona este reto, este cuadrado numérico. Y, a estas alturas, no sólo no lo he logrado, sino que ni siquiera he avanzado.

Estos casi dos meses y medio que no hice aportaciones a esta página, no significan que abandoné mi inquietud. ¡Para nada! He seguido resolviendo sudokus, aplicando estrategias, buscando comprobar procesos mentales que me llevan en una u otra dirección para decidir qué número poner en una celda o cuál candidato quitar. Y sigo tan alejada de mi objetivo: Todavía no entiendo cómo se enredan los números para ofrecernos el reto, ni cómo podría "ver" las opciones lógicas.

Tengo fe en que, si persevero, llegará el momento de la revelación. Sí. Eso creo. ¿Pero si no es así? ¿Todos podremos, o tendremos la capacidad, de resolver un sudoku? 

En el artículo "Trump vs. Sudoku", Jerry Martin -maestro retirado-, considera que hay al menos tres capacidades mentales indispensables para lograrlo. Además asegura -en otra entrevista- que se pueden enseñar a los niños a través del sudoku, pues les permiten "no sólo aprender a razonar, sino a pensar críticamente, a ser exactos y a trabajar (juntos) para resolver problemas. Habilidades que se traducen en muchas facetas de la vida" -dice él. 

Estas capacidades son:

1° Se debe estar 100% seguro al seleccionar cada número. No hay lugar para la inexactitud, esto nos llevaría a equivocaciones, pérdida de tiempo, desgaste, cansancio y cero resultados. (La calidad de la información es importante).

2° Hay que ser capaz de discernir constantemente entre la información relevante y la irrelevante. En cada celda sin llenar habrá candidatos que podrían excluirse -o ignorarse- y que, al hacerlo, nos permiten "ver" al candidato correcto y, por tanto, seleccionarlo. Cosa que no lograríamos si no descartamos información no relevante.

3° No debemos comprometernos a una acción (anotar un número, eliminar un candidato o emplear una estrategia) antes de tener información adecuada. (Y bastante información).

En cuanto a Donald Trump, Jerry Martin afirma que "si él cree lo que dice" en campaña, donde sus declaraciones son inexactas o falsas, además de irrelevantes y con salto a conclusiones prematuras basado en información inadecuada, seguro es incapaz de resolver un sudoku en privado; pues los procesos mentales que crearon estas declaraciones violan los tres requisitos básicos del Sudoku.